 |
| MzSpectralFlux |
|
 |
|
SYNOPSIS
MzSpectralFlux -- Estimates note onsets from changes in spectral magnitudes.
Spectral flux is a measurement of the change in magnitude between frames in a spectrogram. This plugin calculates estimated
note onsets from spectral flux and also demonstrates the various
steps taken to calculate the spectral flux and derived onset times.
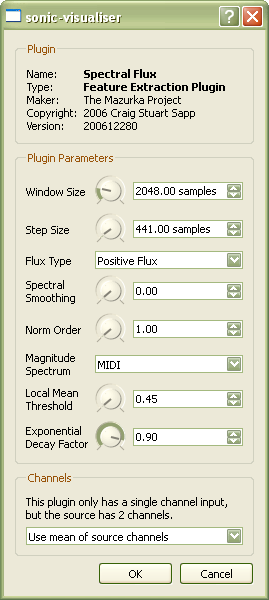
INPUT PARAMETERS
MzSpectralFlux accepts 8 input parameters:
- 1. Window Size
The size of the audio analysis window in samples for
calculating underlying spectra. Window sizes under
1024 samples do not seem to be useful for calculating
the spectral flux. Larger window sizes do seem to
reduce some noise due to beating of partials in
pitched music.
- 2. Step Size
The number of samples between analysis window starting
points. The peak-finding algorithm is currently optimized
to a step size of 10 milliseconds which corresponds
to 441 samples when the sampling rate is 44100 Hz.
Probably not useful to alter this value since some of the
peak finding parameters are not yet adjustable by the user.
- 3. Flux Type
How to process the spectral difference values to generate
a flux value:
- "Total Flux" = use all spectral bin slopes.
- "Positive Flux" = set all negative bin slopes to zero.
- "Negative Flux" = set all positive bin slopes to zero.
- "Difference Flux" = non-negative positive minus negative
flux values.
- "Composite Flux" = a commixture of the first three flux
types: (positive - negative) / (|total - positive|).
- 4. Spectral Smoothing
The amount of smoothing applied to the spectral frames
before the spectral difference is calculated. 0.0 = no
smoothing, 1.0 == infinite smoothing. A value of 0.99
usually works very well.
- 5. Norm Order
The p-value for calculating the norm of the spectral
difference vector.
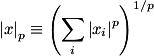 Using p=1 generally gives the best results,
but you can try various values to see for yourself.
Try a
p-value of 1.5, for example.
On the right is
the mathematical definition for the norm which is
used in this plugin, where p is this input parameter
and xi are the spectral difference
values.
Using p=1 generally gives the best results,
but you can try various values to see for yourself.
Try a
p-value of 1.5, for example.
On the right is
the mathematical definition for the norm which is
used in this plugin, where p is this input parameter
and xi are the spectral difference
values.
- 6. Magnitude Spectrum
What type of basis spectrum to use for calculating
the spectral slope data.
- 7. Local Mean Threshold
Used for calculating onset times from the scaled spectral flux
function. This is the value above the local maximum
of the scaled spectral flux function which a value must
achieve in order to be considered a peak. If you have
too many false positive onsets, increase this value;
if you have too many false negatives (missing real onsets),
decrease this value.
- 8. Exponential Decay Factor
Used for calculating onset times from the scaled spectral
flux function. This is the feedback gain for an
exponentially decaying function based on the scaled
spectral flux function. Scaled flux values which
are below the exponential decay function are not
considered when searching for peaks. If you have too
many false positive onsets, increase this value; if you
have too many false negatives (missing real onsets),
decrease this value.
OUTPUTS
MzSpectralFlux generates 6 outputs:
- 1. Underlying Spectrogram
A spectrogram of the underlying spectral data used to calculate
the spectral slope and spectral flux values.
- 2. Spectral Derivative
A spectrogram displaying the differences between successive
spectra (output #1). The slope are also processed with
according to the "Slope Selectivity" input parameter.
Values in the output are normalized for the visual display
enhancement
(but not normalized when calculating the spectral flux values).
- 3. Raw Spectral Flux Function
The basic spectral flux calculated from differences
between successive spectral frames. This is the starting
data for calculating onset times.
- 4. Scaled Spectral Flux Function
The same thing as output #3, but the mean (average) value of the
points in this function is shifted zero, and the values are
also scaled so that the standard deviation of the function is
1.0. This makes the function more amenable to comparisons
between different function generation methods, and well as
for post processing with a peak selection algorithm.
- 5. Exponential Decay Threshold
Underlying data used in identifying peaks in the scaled
spectral flux function. These values are generated by
sending the scaled spectral flux function through an
exponential smoothing function to suppress noise in the
data after in initial onset (noise usually due to
beating partials). The input parameter "Exponential Decay Factor"
is used to calculate the rate of decay after a note attack.
- 6. Local Mean Threshold
Also used to calculate peaks in the scaled spectral flux
function. These values are generated from averaging
in a limited local area on the spectral flux function and
then adding an extra offset parameter set by the user
as input to the plugin.
DESCRIPTION
Spectral flux
Spectral flux is a measure of the change in energy between
various frequency bands in a sequence of spectra measured
from the audio data.
Spectral flux is calculated in three steps:
- Calculate a sequence of spectra.
- Measure the difference between successive spectral bins.
- Collapse the spectral difference of selected bins (from #2) into a
single spectral flux value.
The resulting spectral flux function can then be used to identify
onset times for notes in the audio data by searching for peaks
in the spectral flux function.
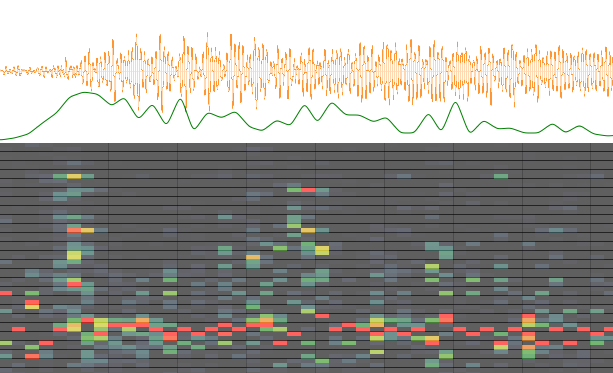
Here are some of the example steps in calculating the
spectral flux function. The following figure contains the
original waveform in orange. Underneath the waveform is the
corresponding spectral flux function in green. And underneath
the spectral flux function is a display of step #2 in calculating
the spectral flux function -- the difference spectrogram.
Flux variants
Spectral flux is defined most simply as the Euclidean
distance between successive spectral frames:
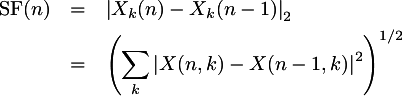
This form of spectral flux is a bit noisy due to the
equal emphasis on rising and falling spectral energy. If you
want to locate note onsets, then you should instead
look at only the positive values in the spectral difference:
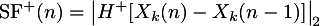 Where H+(x) = (x + |x|)/2
is the positive half-wave rectifying function which sets negative
values to zero, and leaves positive values unaltered.
Where H+(x) = (x + |x|)/2
is the positive half-wave rectifying function which sets negative
values to zero, and leaves positive values unaltered.
There is also negative spectral flux which is usually not
interesting by itself:
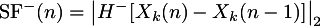 where H-(x) = (x - |x|)/2
is the negative half-wave rectifying function which sets all positive
values to zero and leaves negative values unaffected.
where H-(x) = (x - |x|)/2
is the negative half-wave rectifying function which sets all positive
values to zero and leaves negative values unaffected.
Note that SF+(n) + SF-(n) = SF(n). This is sometimes interesting to consider, so give it
the name difference flux:
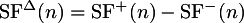
Usually it is best if you limit values of SFΔ to
non-negative values by setting the negative values to zero:

And finally, consider the composite flux which is defined as:
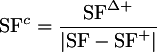
This form of spectral flux may be interesting, but is difficult to
extract peaks in the same manner as the other types of spectral flux.
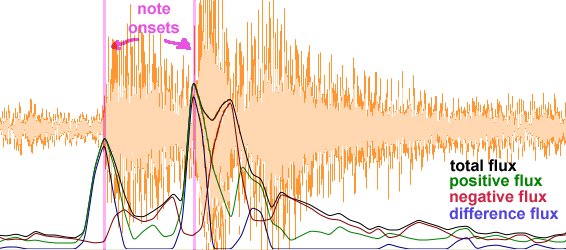
Here are visual examples of the first four types of flux. The
black curve represents the total flux, the green curve the positive
flux, the red curve the negative flux and the blue curve the
difference flux.
correlation spectral flux
Instead of subtracting adjacent spectral frames to
derive a spectral flux value, the change in correlation between
three successive spectral frames can be compared:
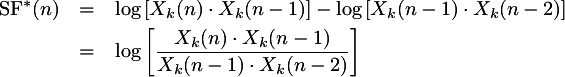 Where:
Where:
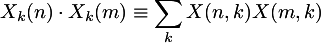 is called the dot product, or alternatively unnormalized correlation.
Taking the logarithm of the dot product calculations is necessary to have
the spectral flux analygous in range to the standard flux definitions
which subtract adjacent spectra rather than multiply spectra together.
is called the dot product, or alternatively unnormalized correlation.
Taking the logarithm of the dot product calculations is necessary to have
the spectral flux analygous in range to the standard flux definitions
which subtract adjacent spectra rather than multiply spectra together.
This method of calculating spectral flux shows potential, but
needs some fine-tuning.
angular spectral flux
The dot product can also be defined as:
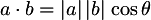 It is interesting to look at changes in the angle in isolation
rather than changes in the correlation which is a mixture of
the angular and magnitude changes.
It is interesting to look at changes in the angle in isolation
rather than changes in the correlation which is a mixture of
the angular and magnitude changes.
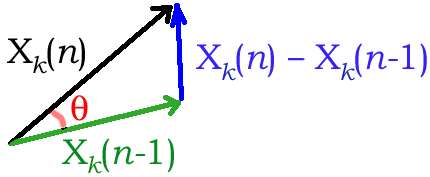
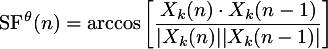 Angular spectral flux is also related to subtractive spectral
flux as illustrated in the following figure. The current spectral
frame can be considered a vector (colored black in the example) as
well as the previous spectrum (colored green in the example).
The standard definition of spectral flux looks at the changes in the
difference between the two spectra which is equivalent to the
vector pointing from the previous spectrum to the current spectrum
(colored in blue).
Angular spectral flux is also related to subtractive spectral
flux as illustrated in the following figure. The current spectral
frame can be considered a vector (colored black in the example) as
well as the previous spectrum (colored green in the example).
The standard definition of spectral flux looks at the changes in the
difference between the two spectra which is equivalent to the
vector pointing from the previous spectrum to the current spectrum
(colored in blue).
Angular flux shows promise, but gives too many false positives
in its basic form, and would need to be refined to make it useable
for detecting note onsets. Problems to consider: phase wrapping
might be causing lots of the noise in this method.
Slightly better peak-to-noise behavior occurs when just
using the raw cosine of the angle between the two spectra:
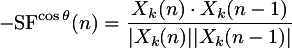
(don't know why the negative sign is needed, but it is).
Both the angular flux and the cosine flux can generate weird
oscillations occasionally during a sustained tone. Fix that
problem and they might be useful measures of note onsets...
L-norm selection
The Euclidean distance used in the previous section definitions
of spectral flux is usually not the best method of collapsing the
spectral difference values into a single number. In general
it is better to just sum the spectral difference values together
rather than square each one, then add, then take the square root
of the sum:
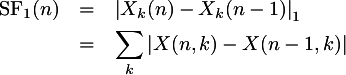
In engineering terms, the Euclidean distance is called the
L-2 norm, and summation is the L-1 norm, where the norm is
defined by the following equation:
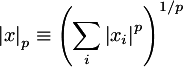 where xi is a sequence of numbers to norm, and
p is the norm level. For Euclidean distance, or L-2 norm, p=2.
For summation, or L-1 norm, p is 1. A generalized equation
for the spectral flux using any possible norm would then be:
where xi is a sequence of numbers to norm, and
p is the norm level. For Euclidean distance, or L-2 norm, p=2.
For summation, or L-1 norm, p is 1. A generalized equation
for the spectral flux using any possible norm would then be:
In general, the smaller the value of p in the above
equation, the better the peak behavior in the spectral flux function.
In the following example, the p value is varied to display
the differences in the scaled spectral flux function.
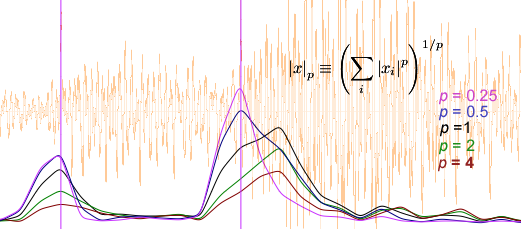
Notice that lower values of p usually give better
resolution of the start of an attack, such as in the second
onset identified in the above example.
Spectral smoothing
Smoothing the spectral frames before calculating the
spectral differences can help to remove noise in the spectral
flux function. Usually a high amount of smoothing can remove
most false-positive detected onsets.
The following figure shows an example of the effect of
smoothing on three attacks in a piano recording. Five
scaled spectral flux functions are displayed using the
following smoothing factors: 0.0 (no smoothing), 0.5, 0.75, 0.9 and
0.99. Notice that the more smoothing that is applied to the
spectral frames, the higher the peak at the attack points
(purple vertical lines). This allows for a higher local maximum
threshold (0.85 in this example) and also a higher exponential
decay value (0.95 in this case).
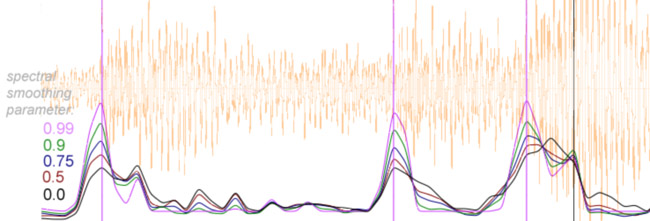
Applying spectral smoothing is similar in effect to
positive flux calculation. The total flux and positive flux are
nearly identical with strong spectral smoothing.
Peak detection
To estimate note onset times in the spectral flux function,
three rules are applied to identify peaks in the spectral flux
function which are assumed to correspond to note onsets in the
audio:
- Local maximum: A value in the spectral flux function must
be equal to the maximum value in the range of +/- 30 milliseconds
(+/- 3 values with a 10 millisecond frame rate).
- Exponential decay threshold: the test peak must not be
less than an exponential decay curve fitted to the spectral
flux function. The exponential decay curve is defined as:
g[n] = max(f[n], a g[n-1] + (1-a) f[n]), where g[n]
is the threshold function, f[n] is the spectral flux function,
n is the time index, and a is the exponential decay
factor.
- Local mean threshold: the test peak must be greater
than the local mean plus an extra offset factor. The local mean
is the average between -90 milliseconds and + 30 milliseconds.
The following example image shows the two threshold functions
along with the spectral flux function and the detected onset peaks.
The spectral flux function is the thin blue line with the dots at
each measured point (10 milliseconds apart). The local mean threshold
function is the lower solid curve colored in red. The exponential
decay threshold function is the upper solid curve colored in green.
Identified onset times are highlighted with purple vertical lines.
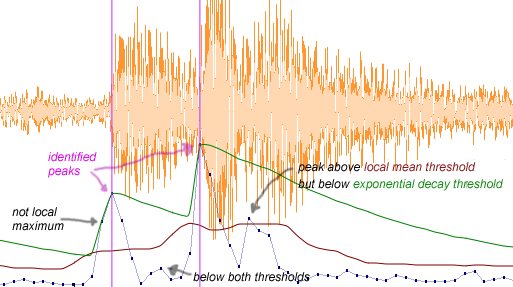
Note that there is a fairly large peak after the second onset.
While this peak does go above the local mean threshold, it does not
get as high as the exponential decay threshold. Therefore it was not
identified as an onset peak. Also note the small peak between
the first and second detected onsets. While this peak contains
a local maximum, it neither rises above the local mean threshold nor
meets with the exponential decay threshold, so it is not considered
an onset event.
Here is another example of the two threshold functions along
with the spectral flux function and detected onsets:
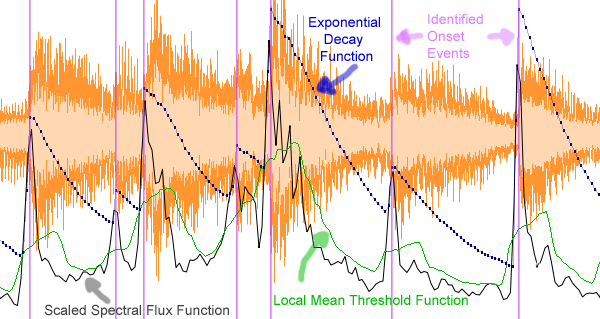
REFERENCES
Dixon, Simon. "Onset detection revisited" in the Proceedings of the
9th International Conference on Digital Audio Effects (DAFx'06). Montreal,
Canada; September 18-20, 2006.
[Slides]
DOWNLOAD
| 



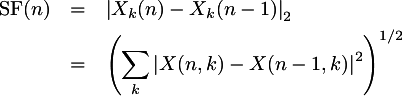
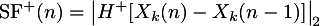
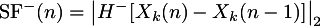
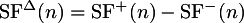

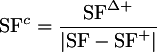

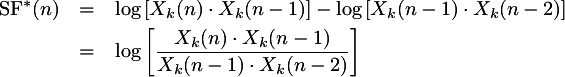
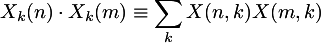
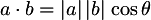
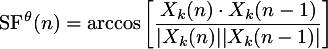

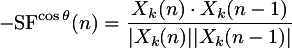
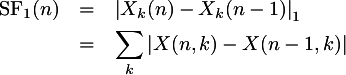
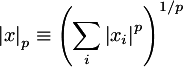
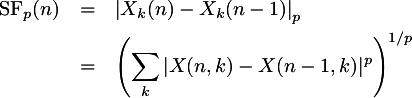



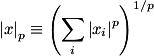 Using p=1 generally gives the best results,
but you can try various values to see for yourself.
Try a
p-value of 1.5, for example.
On the right is
the mathematical definition for the norm which is
used in this plugin, where p is this input parameter
and xi are the spectral difference
values.
Using p=1 generally gives the best results,
but you can try various values to see for yourself.
Try a
p-value of 1.5, for example.
On the right is
the mathematical definition for the norm which is
used in this plugin, where p is this input parameter
and xi are the spectral difference
values.


