MzHarmonicSpectrum

SYNOPSIS

MzHarmonicSpectrum -- Displays the Harmonic Product Spectrum from which pitch estimates of monophonic harmonic input audio can be made.

MzHarmonicSpectrum generates 3 outputs:

1. Harmonic spectrum

The full harmonic product spectrum.

2. Spectral power

The average power of each spectral frame.

3. Raw pitch

Basic estimate of the pitch extracted from the spectrum.

The harmonic product spectrum (or harmonic spectrum for short) is the geometric mean of amplitudes of the harmonics associated with a particular frequency in the spectrum:


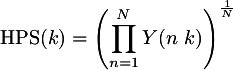
where HPS is the harmonic product spectrum, k is the k-th indexed frequency bin in the harmonic spectrum, Y is the magnitude spectrum of the positive frequencies, and N is the number of harmonics to consider.

The following schematic demonstrates how the harmonic spectrum is calculates. The original spectrum is squeezed so that each successive harmonic of the original signal is aligned with the fundamental harmonic. To do this, the spectrum is squeezed by 1/2 to align the first overtone with the fundamental (it doesn't matter what frequency the fundamental is at because the first overtone is always twice the frequency of the fundamental). Then the spectrum is squeezed to 1/3 to align the second overtone with the fundamental, and so on (typically for about 5 harmonics).



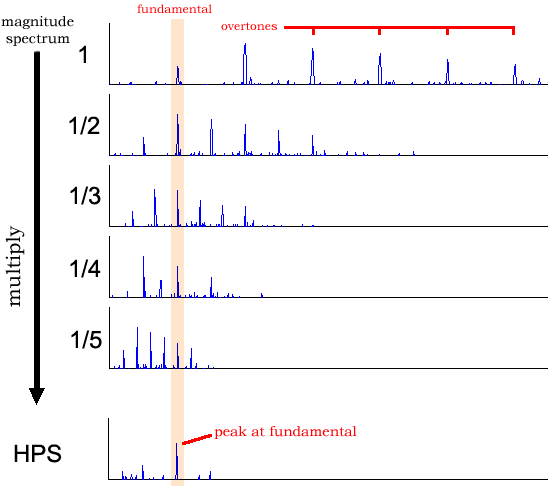
Here is a comparison of the plain magnitude spectrum and the harmonic product spectrum:



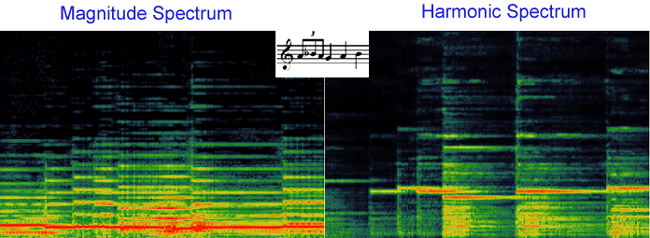
The nice property of the harmonic spectrum is that it gives a simple estimate of the pitch in the audio signal.

Currently under development. Pitch estimate needs elaboration, just finding the max at the moment but need to correct for sub-harmonics which are really the fundamental.

Compiled versions of the MzHarmonicSpectrum plugin can be downloaded from the download page.

The source code for the plugin was last modified on 24 Jun 2006.

• Header:          [ html | PDF | text ]
• Source Code: [ html | PDF | text ]